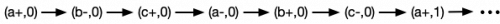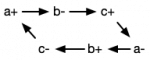
To understand how timing analysis for asynchronous circuits works, let's take a very simple example of a ring oscillator.

if the inverter ring is oscillating, and we make the standard assumption that each signal transition has a fixed delay, then the oscillations of the inverter will have a periodic pattern in time. This basic idea is in fact much more general, and one can show that asynchronous circuits exhibit this sort of periodicity, and it is possible to define the cycle period (or cycle time) of an asynchronous circuit. This cycle period consists of the sum of a number of gate delays.

Now consider the following circuit. This can be viewed as two ring oscillators, except that one of the gates is an inverting C-element that couples the two oscillators. (Recall that a C-element waits for both inputs to change before its output changes.)

What happens if we make one of the ring oscillators slower? The C-element will wait for the slower of the two oscillators before changing its output. Hence, the cycle period of this particular circuit will be determined by the slowest cycle of gates in the circuit. This simple example and intuition can be translated into a rigorous mathematical framework, where we can show that an asynchronous circuit will exhibit periodic behavior¹⁾²⁾ and that the period is determined by the slowest cycle of gates that oscillate.

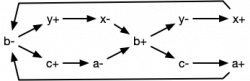
The delay of rising and falling transitions of a gate can be different and depend on the circuits used to implement the gate. When determining the timing of signal transitions, the rising and falling transitions of gates are treated separately. For example, the ring oscillator example above would be translated into the following graph of signal transitions.

The arrows capture dependencies: for example, the graph constraints mean that the downgoing transition of b occurs only after the upgoing transition for a. The equivalent graph for the two coupled oscillator example is:

There is one important detail missing from the graphical representation that we have so far, namely: where does the oscillation start? A more precise way to think about this is to observe that there are many a+ transitions: the first one, second one, third one, etc. If we include the occurrence index for each signal transition, and assume that the first transition that occurs is a+, then we get an acyclic graph that is infinite, like the one below for the ring oscillator.

Each of the labelled transitions (a+,0), (a+,1), etc. are called events, and each of them have a time associated with when they occur. Static timing analysis aims to compute the times at which all the events in the asynchronous circuit occur.

Notice that this graph can be obtained from the original cyclic graph of signal transitions by applying the following steps:

• Deleting the edge from c- to a+
• Creating copies of the resulting graph, except each copy uses a different integer index for each signal transition (so a+ would be mapped to (a+,0) in the first one, (a+,1), in the second copy, etc.)
• Replacing the deleted edge but instead of creating a cycle, using it to connect (c-,i) with (a+,i+1)

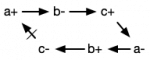
The same information can be represented directly on the cyclic graph of signal transitions by marking the c– to a+ edge with a tick as follows.

This is sometimes called a repetitive event-rule system, and corresponds to the timing graph for the ring oscillator where the first transition is a+. We say that the timing arc from c- to a+ is a ticked edge in the timing graph.

The final ingredient needed to determine the cycle period is the delay of each transition. This can be computed in the same way as it is computed in synchronous static timing analysis. The baseline timer in the ACT flow (cyclone)³⁾ uses the standard NLDM (non-linear delay model) model, which models the delay and transition time of the output of a gate using a table that is indexed by the input transition time and output load capacitance. (NLDM interpolates between data points in the table using standard bi-linear interpolation.) Cyclone takes a Liberty file (.lib) as input for this purpose.

To determine delays, we need to know the slew rate (equivalently, transition time) of all the signals in the circuit during steady-state execution. Cyclone can compute this in two ways: (i) by using interval analysis to compute a narrow delay interval that corresponds to the steady-state transiltion time based on the topology of the circuit; or (ii) by using the reset release transition to compute the the steady-state transition times. Given the steady-state transition times, all signal delays can be computed using the Liberty file.

A particular cycle of transitions in the timing graph imposes a constraint on the cycle period: namely, the cycle period must be at least the sum of the delays around the specific cycle divided by the number of ticked edges on the cycle. In our simple examples above, all simple cycles had only one ticked edge; in general, this need not be the case. The overall cycle period of the entire circuit is the maximum value of the cycle period constraints for every simple cycle in the graph. The cycle in the timing graph corresponding to the cycle period of the overall system is called the critical cycle.

What happens if a cycle in the timing graph has zero ticks? It turns out this cannot happen in any correct timing graph for a circuit. If this occurs, Cyclone will detect it and report it as an error (an unticked cycle).

Suppose the critical cycle has two ticks, and the cycle period is p. Suppose a+ is a signal transition in the circuit. In this case, the time at which a+ occurs will eventually become periodic. Since the there are two ticks on the critical cycle, all we can be certain of is that the gap between (a+,2i) and (a+,2i+2) will eventually stabilize to 2p, and (a+,2i+1) and (a+,2i+3) will also stabilize to 2p. However, the gap between (a+,2i) and (a+, 2i+1) need not be p. In general, if there are M ticked edges on the critical cycle, then we are guaranteed periodicity only between occurrences of a signal transition that are M indices apart. In other words, the number of ticks on the critical cycle determines the nature of the periodicity of the circuit. Cyclone computes and reports both p and M during static timing analysis.

The Cyclone static timing analysis engine reports the delay offset relative to M*p. So, for a particular signal transition like a+, there will be M offsets reported.

In the examples above, it was clear where the ticks in the timing graph should be placed. However, in a general asynchronous circuit, determining the placement of ticks after-the-fact is a non-trivial problem. In fact, techniques for doing this that are known (e.g. described in the Cyclone paper) have a computational complexity that is comparable to state-space exploration. Also, they use information that is in fact computed during logic synthesis of asynchronous circuits! Hence, the ACT flow assumes that tick placement is computed and generated during the logic synthesis process. These tick specifiers are included in the ''spec'' sub-language.

Placing ticks in the right location is probably the most confusing aspect of building a correct timing graph for asynchronous circuits. What follows are some rules of thumb that should help you with this process. Note that if you are using our logic synthesis tools, they automatically tick the appropriate edges in the timing graph, so this section need not concern you. However, if you are generating your own asynchronous design via some alternate approach, then you will need to develop a strategy for ticking the appropriate edges in the timing graph.

Let's consider a simple example of a handshake protocol between two processes shown below.

In this example, the handshake starts with the request going high (req+). This means that the ticked edge would be from ack- to req+, since the ith transition of ack- results in the (i+1)th transition of req+. Alternatively, the process might reset with req high (e.g. if the process P1 begins with a token on its output). In this case, the timing graph would have a different edge ticked as shown below.

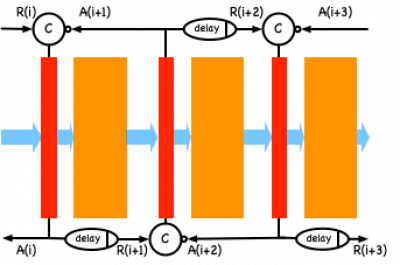
As a concrete example, consider the classic micropipeline circuit topology shown below.

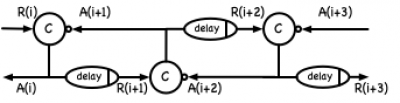
In this simple linear pipeline with no data-dependent control, the handshake signals are simply used as triggers for the datapath storage elements. Simplifying the logic to just the control gives us:

Initially all signals are low, and the pipeline operation is initiated by the environment setting the input request high. This causes the first C-element to change its output. This means that the timing graph path from R(i)+ to A(i)+ does not have any ticks on it. However, there is also a timing arc from A(i+1)- to A(i)+ (the “bubble” input of the C-element). Since A(i+1) is initially low, this means that the C-element waits for A(i+1) to be low from the previous iteration of the handshake! Hence, the A(i+1)- to A(i)+ arc would be a ticked edge. Note that this is consistent with the simple handshake example above, looking at the request/acknowledge pair R(i+1) and A(i+1).

Another example of where ticks get inserted is when looking at gates that have the chip reset as their input. When reset is released, some of these gates initiate a transition. These initial transitions are good candidates to look at carefully to see if their input timing arcs should have ticked edges.

Ticks are fungible; if all the inbound edges to a vertex in the timing graph are ticked, that is equivalent (from a timing analysis perspective) to adding a tick to all the outbound edges from the vertex (and eliminating the inbound ticks). While in general an edge could have multiple ticks, Cyclone restricts its attention to timing graphs where each edge has at most one tick. (This can be worked around easily if needed.)

In the simple linear pipeline example above, none of the datapath logic would have ticked edges since the ith datapath input change for the storage elements propagates to to the ith output change, and through the combinational logic.

However, if instead we have a token ring, that token ring would have some datapath element (and the control handshake) that initializes with a token on its output and valid data in the datapath. For that particular datapath storage element, we would tick the data input to the storage element.

If a timing graph has a cycle of arcs with no ticks, this corresponds to an asynchronous circuit that is deadlocked–i.e. that does not oscillate. If this is detected, Cyclone will report an unticked cycle and display the cyclic path in the timing that is problematic and then stop.

We also provide a “catch-all” tick placement approach that ensures that every cycle in the timing graph has at least one tick. To turn this option on, set the integer configuration option timer.fixticks to 1. This can be done via a run-time configuration file, or using the interact command

interact> conf:set_int "timer.fixticks" 1

prior to running the timing graph construction pass.

Note: using the fixticks option may not result in the correct placement of ticks, and could lead to a performance estimate that is erroneous.